이진 트리 배열의 DFS - 1 (Binary Tree Array)
이번 글에서는 스택이나 재귀함수 없이 깊이 우선 탐색을 이진트리에 적용하려고 합니다.
이진 트리 배열
이것이 이진 트리입니다.

0 은 루트노트(root node).
0 은 두개의 자식노드(children node)를 가지고 있습니다: 왼쪽 1, 오른쪽 2
각각의 자식노드는 또다시 자신의 자식노드를 가지고 있습니다. 이러한 노드들을(3,4,5,6) 리프 노드(leaf nodes)라고 부릅니다.
루트와 리프노드 사이의 있는 간선(edges)의 갯수가 이진트리의 높이를 결정합니다. 위의 트리에서는 높이가 2입니다.
일반적인 이진트리의 접근법은 BinaryNode라는 클래스를 만들어줍니다.
public class BinaryNode<T>{
public T data;
public BinaryNode<T> left;
public BinaryNode<T> right;
}하지만, 이진트리를 배열을 이용해서 접근하는 방법이 있습니다. 만약에, 이진트리를 레벨별로 나누어서 루트노드부터 열거한다면, 배열을 이용해서 이진트리를 나타낼 수 있습니다.

부모인덱스와 자식인덱스의 관계를 통해 부모노드에서 자식노드으로, 자식노드에서 부모노드로 이동할 수 있게 해줍니다.
parent(i) = ( i - 1 ) / 2
left_child(i) = 2 * i + 1
right_child(i) = 2 * i + 2염두해야 할것은, 트리는 완전이진트리 (complete binary tree)이여야 합니다. 이것은, 이진트리의 특정 높이에서 배열 요소의 갯수를 계산 할 수 있기 때문입니다. 특정 높이에서 배열요소의 갯수는 2^(height+1) - 1 입니다.
예를 들어, 높이가 2인 이진트리의 배열요소의 갯수 : 7개
-> 2^(2+1) - 1
-> 2^(3) - 1
-> 8 - 1
-> 7
빈 노드에는 null을 배치함으로써 충족조건을 만족시키고, 이진트리를 배열의 형태로 만들 수 있습니다.
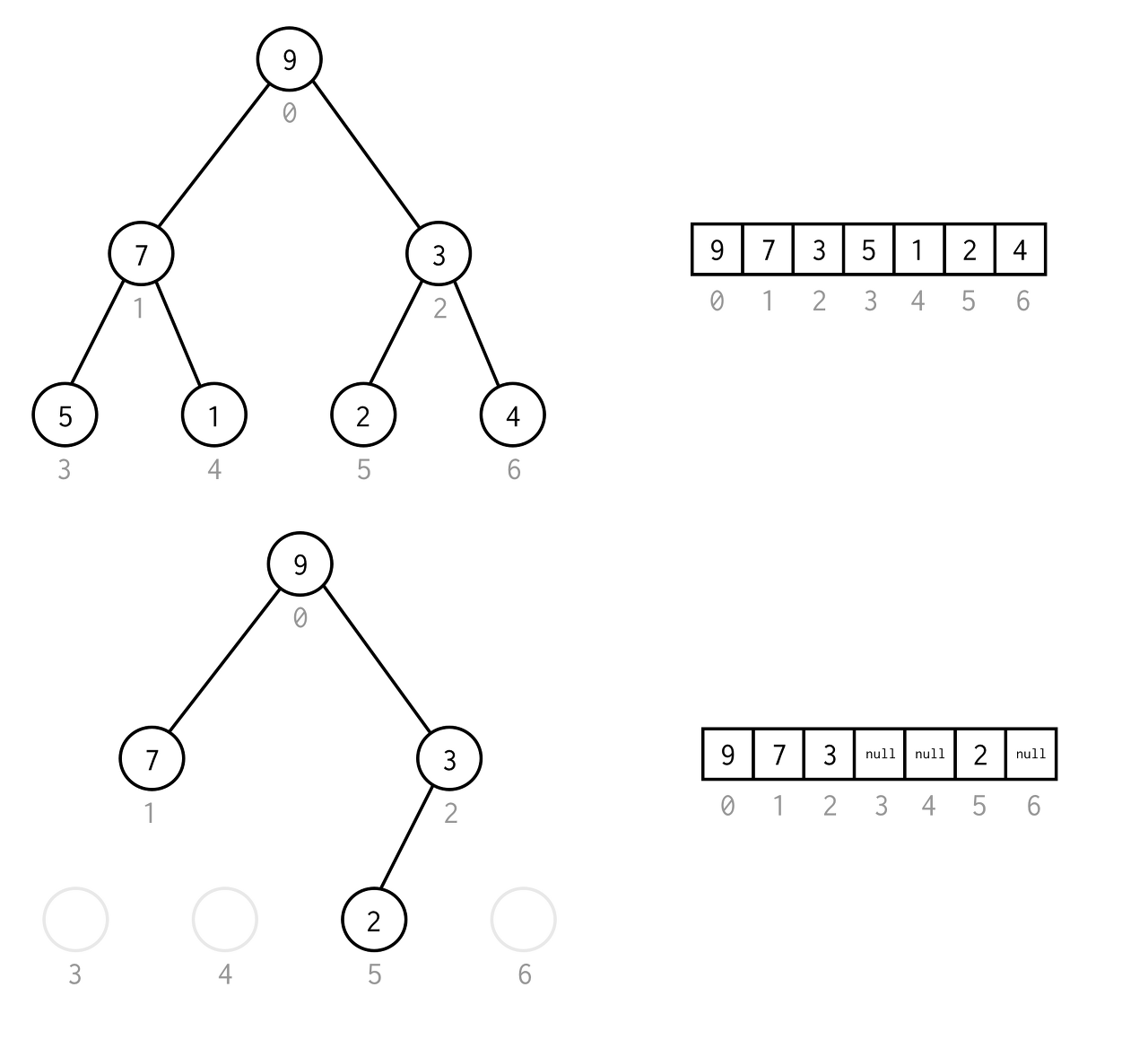
배열이 이진트리를 나타낸 것을 우리는 이진 트리 배열(Binary Tree Array)이라고 부릅니다. 이것은 항상 2^n-1 갯수의 배열 오소를 가지고 있다. 즉, 이진트리의 배열 요소의 갯수는 1, 3, 7, 15 ... 개 가 있다.